Ziegler-Natta heterogeneous catalysis is nowadays the most important industrial process for the production of polyolefins by polymerization of terminal alkenes. The constituents of the solid catalysts are MgCl2 as a support, TiCl4 as an active precursor in combination with a cocatalyst, such as triethylaluminium, Al(C2H5)3 which serves as a Lewis base or donor. The latter exerts a steric and electronic influence on the active sites (alkylated Ti+3) improving their stereoselectivity. The substrate plays a crucial role both at the formation of the catalyst sites and in the polymerization process. Over the past few decades, supported catalysts systems have had a great effect in improving the efficiency of polyolefins production, with enormous economic impact. Polyethylene and polypropylene are the two most widely produced commodity plastics. They have numerous industrial applications in the packaging, construction, electrical & electronics, automotive, healthcare & pharmaceuticals, agriculture, as well as in the polymer industry for the production of high density polyethylene, the manufacture of thermoplastic polyolefins, or ultra-high molecular weight polyethylene. In 2019, the global polypropylene market was worth $126.03 billion and that for polyethylene $163 billion.
The Challenge
The development of industrial Ziegler-Natta catalysts has been predominantly a matter of trial and error. Obtaining deeper understanding of these catalysts is crucial for the rational improvement of the industrial process. In particular, it is essential to unravel the basic steps in the catalytic process and to identify the structure of the active centers and the role of the supporting material. In silico computational studies can be extremely useful in assessing the different steps of the chemical process and the corresponding reaction rates. As such, modeling the reaction mechanisms at atomic level can provide critical insights about the activity and selectivity of the catalyst, which cannot be obtained experimentally.
The Work
In the present case study, we investigate the initial reaction of Ziegler-Natta propylene polymerization by density functional theory (DFT) calculations using the Quantum Espresso plugin in MAPS. The transition state search was performed with the Nudged Elastic Band method. Geometry optimizations of the slabs were performed using ultrasoft pseudopotentials with the plane wave/density cutoffs of 900/9000 eV and sampling at the Γ-point, along with the PBE exchange-correlation functional and the semi-empirical Grimme D2 dispersion correction.
The Results
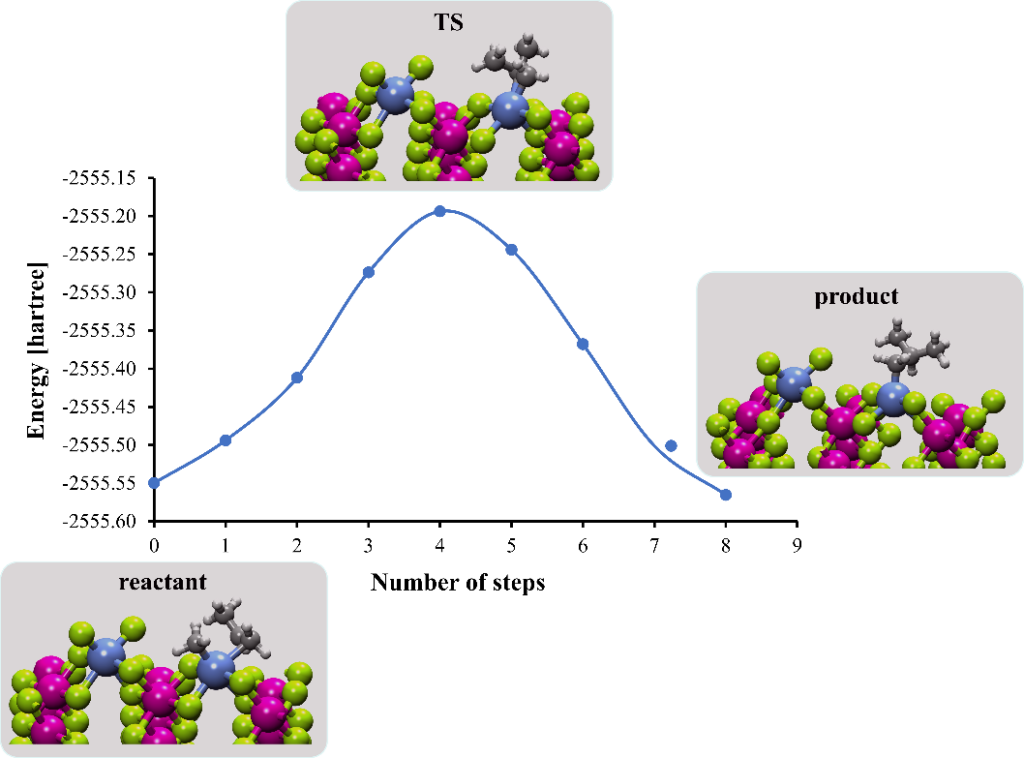
First, the structure of the reactant system, which is a Ti-based catalyst supported on MgCl2 was obtained. The bulk structure of MgCl2 was optimized with respect to the kinetic energy cutoff and the Brillouin zone sampling to values of 900 eV and 4 × 4 × 4 k-point grid, respectively. The optimized cell parameters (a = b = 3.669 Å and c = 6.093 Å) are in excellent agreement with the experimental values (a = b = 3.641 Å and c = 5.927 Å). A TiCl4 molecule was deposited on the 2 × 3 supercell of MgCl2(110) surface. Ti appears in a 6-fold coordination, as a replacement of the Mg atom in the MgCl2 structure. The reactant was obtained by replacing two Cl atoms by -CH3 and -C3H6 groups, representing the chain terminator and the approaching propylene, respectively. The optimized structures of reactant, product and transition state and the energetics are shown in Figure 1. The initial propylene reaction is exergonic with a free energy of -16.7 kcal mol-1 and a transition state barrier of 10.8 kcal mol-1. It is interesting to note that the active center in the product is unshielded and available for subsequent insertion and complexation process toward polypropylene formation.
Figure 1: Reaction pathway of the initial propylene insertion in Ziegler-Natta catalysis.
In silico modeling studies are nowadays an indispensable part of the cutting-edge research in catalysis, providing understanding of observed trends and predictions toward rational design of the next generation catalysts.
- Boero, M.; Parrinello, M.; Hüffer, S.; Weiss, H. J. Am. Chem. Soc. 2000, 122 (3), 501–509. https://doi.org/10.1021/ja990913x.